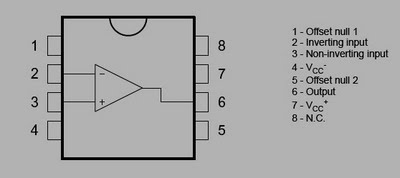
Operational amplifier also known as Op Amp is one of the most useful, analog circuit element. It has many uses, such as an amplifier, a buffer, an inverter, an integrator, a differentiator, an oscillator, a comparator and more. Since it is so versatile, it is used in all kinds of applications. Therefore understanding Op amp and its working is importance as an electronics engineer.
This article will explain
- What is Operational amplifier
- Characteristics of Operational amplifier
- Working of Operational amplifier
- Operation modes of Operational amplifier
- Applications of Operational amplifier
What is Operational amplifier
Op Amp is an integrated circuit ( IC ) which is used to amplify weak signals in analog circuits. A single Op amp unit has two inputs and one output pins. One of the input is called as Non-inverting or positive input while the other input is referred as Inverting or Negative input. In a nutshell, Operational amplifier can be described as a component which outputs the amplified version of the voltage difference between the signals applied in its positive and negative input.
Important characteristics of Operational amplifier
These are the most important characteristics of Op amp.
- High input impedance – This enables Op amp to draw low current in its input pins and makes it suitable to function as an amplifier.
- Low output impedance – This enables Op amp to provide maximum current it its output pin to drive high power load. This again is a necessary quality for an amplifier.
- High gain – Op amps have high gain which means it is capable of amplifying weak low voltage input signals effectively to high voltage output signals.
- High frequency response – Op amps are versatile to operate on wide range of input signal frequencies.
Working of Operational amplifier
There are several things that are basic to understanding op amps and their operation. The circuit in Figure 0 shows the symbol for the op-amp, U1, and a simplified schematic of the insides of an op-amp. The Op amp has a positive and negative power connection. This provides power from a power source to operate this device.
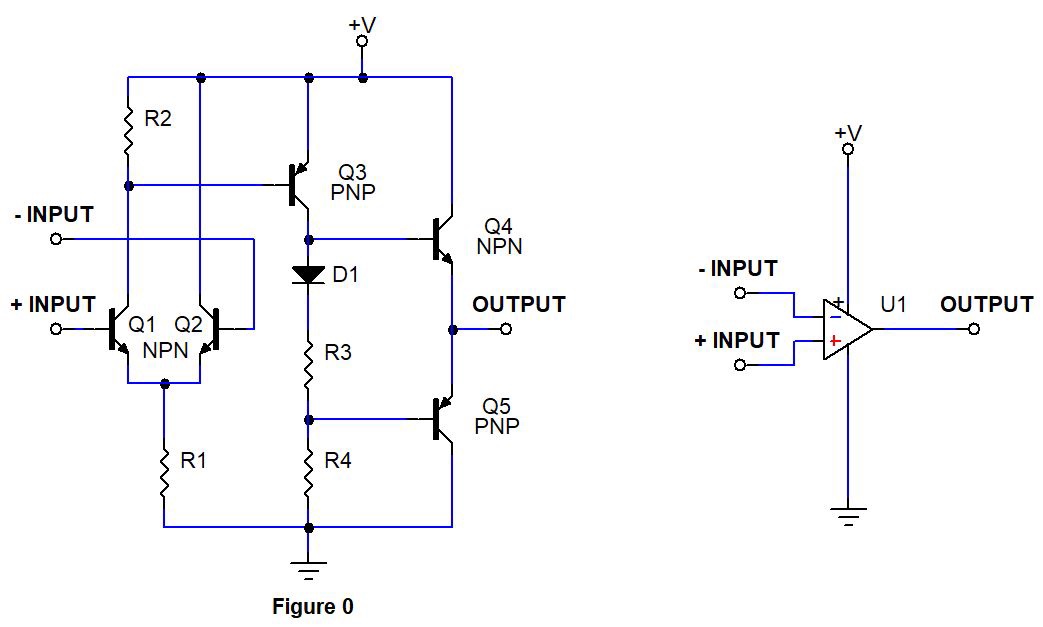
Single or split power supplies can be used depending upon the application. The Op amp has three signal terminals, a positive signal input, a negative signal input, and the op-amp signal output. An op-amp consists of a differential input stage made out of transistors(Q1, Q2), a level shifter stage Q3, and an output stage (Q4, Q5), as shown in Figure 0.
When positive voltage is applied to + Input that is Q1 base and – Input tied to ground, Q3 will be activated ( read about working of transistors to understand this better ). This allows current flow from emitter to collector terminal of Q3. As a result positive voltage will be developed across R3 and R4. This voltage activates Q4 and output will exhibit +V voltage level.
On the other hand when positive voltage is applied to – Input and + Input tied to ground. Q3 will not be activated, hence Q4 will be in off state, however Q5 will turn ON since it is a PNP transistor and low logic at its base activates them. Now Output pin will exhibit low state and Q5 provides a current sinking path through its Emitter to collector terminal.
Operation modes of Operational amplifier
Operational amplifier operates in two modes. They are Open loop and Closed loop operation.
Open loop operation: This is the operation mode where output signal from output terminal of Op amp will not be fed back to it’s input terminals. When there is no feedback, the Op amp acts as a comparator (explained later ).
Closed loop operation: This is the operation mode where output signal from output terminal of Op amp is fed back to input terminals of Op amp.
There are two ways in which we can configure Closed loop operation of an Op amp. They are Positive and Negative feedback.
Positive feedback
When there is feedback to the positive input, this is called positive feedback and is used in oscillator circuits, or used for hysteresis in comparator circuits. Because of the high internal gain of the op-amp, when the positive input is more positive, greater than the negative input, the output will be fully positive. When the positive input is less positive than the negative input, the output will be fully negative.
Negative feedback
When there is feedback from the output to the negative input, this is referred to as negative feedback and is commonly used in amplifier applications. The most important thing to remember is when using negative feedback, Op amp will force the input voltages at positive and negative terminal to be equal.
Also read:
- Resistors: Working and Applications in circuits
- Capacitors: Working and Applications in circuits
- Inductor: Working and Applications in circuits
How to use Operational amplifier in Circuits
Applications of Operational amplifier ranges from filters, rectifiers, amplifiers, signal generators, modulators circuits and much more. The below listed applications will help you to understand how to use Operational amplifiers in circuits in the way you intended.
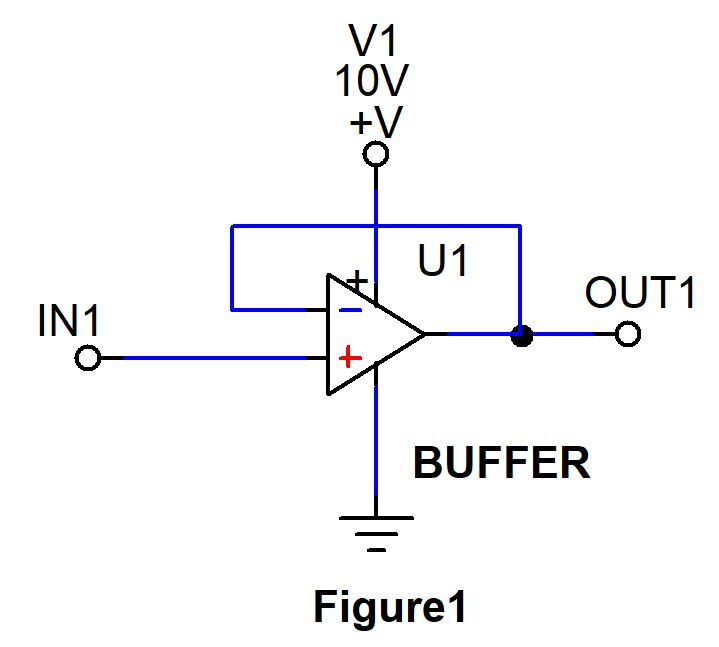
1. Buffer
The first one is the buffer, this is the simplest of all uses. Buffer is used to link series of amplifier circuits together without having to worry about impedance. It essentially amplifies the current or power of an input signal. Since the input impedance of Op amp is high, signal with very less current can be used as input. Also output impedance of Op amp is low hence output signal will have high current. This makes Op amp a perfect buffer.
The signal to be buffered is applied at the positive input. Here negative feedback is a direct connection from the output to the inverting input, therefore output will follow the input signal fed to the positive terminal of Operational amplifier. This is done to keep the voltage at positive and negative input equal. This circuit provides unity gain (1X) and buffers a weak input signal to a strong, buffered, output signal.
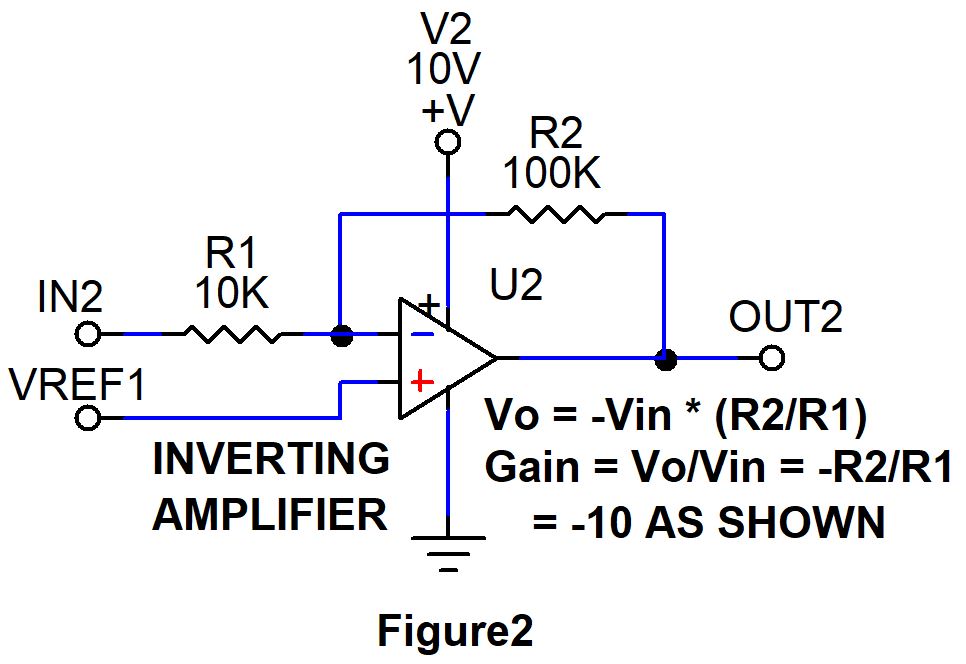
2. Inverting Amplifier
The second basic circuit is an inverting amplifier. Refer to Figure 2 for the following discussion. The input signal is connected via an input resistor R1 to the negative input of the Op amp. R2 is connected from the negative input to the output of the op amp. The positive input can be connected to ground or to a reference voltage.
The Op amp inverts the input signal and amplifies it according to the formula,
Vo = VREF1 + (Vin * (-R2/R1))
where, Vo = Output voltage and Vin = (VREF1 – Vin2).
The example in Figure 2 shows an amplifier gain of -10.
If VREF1 = 2V and IN2 = 2.1 V, then Vo = 2V + (2V – 2.1V) * 100K.10K = 1 volt.
When we use split power supplies and VREF1 is connected to ground, Then the simplified formula in figure 2 would apply. If the gain of the inverting amplifier is equal to one, we call it an inverter.
The inverting amplifiers are widely used where the Opamp provides controlled amplification of the input signal. In theory Operational amplifiers has infinite gain therefore without the use of Negative feedback the input signal will have unpredictable gain and therefore output signal swing to maximum voltage equivalent to supply voltage or V2 ( 10V in the above figure ) of Op amp chip itself. The negative feedback configuration used in the inverting amplifier prevents this and provides controlled amplification of the input signal.
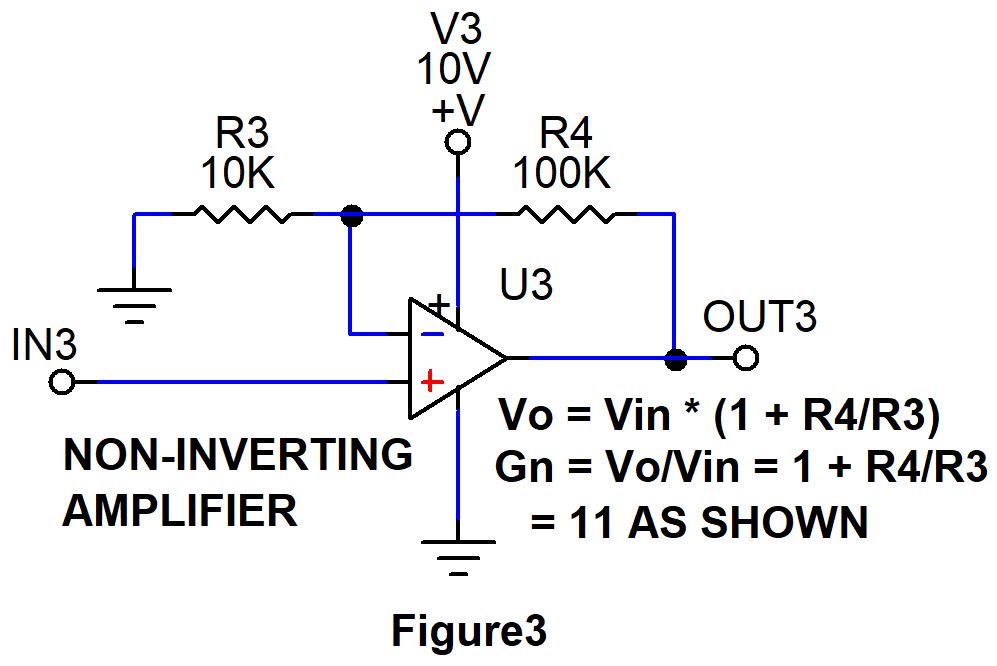
3. Non-Inverting amplifier
The third basic circuit is a non-inverting amplifier or simply an amplifier. Refer to Figure 3 for the following discussion. The input signal at IN3 is connected to the positive input of the operational amplifier. Resistors R4 and R3 form a resistive divider to provide feedback to its negative input.
As we read earlier the op amp will try and force to make the inputs to be equal in amplitude. Therefore when 100mV is applied to the positive input, the op-amp will try to make the minus input equal to 100mV via the feedback network.
The output voltage of Op amp is governed by the formula
Vout = Vin * (1 + R4/R3)
In this example, Vout = 100mV * (1 + 100K/10k) = 1.1 volts.
Here the gain of this amplifier is given by R4/R3 to 10.
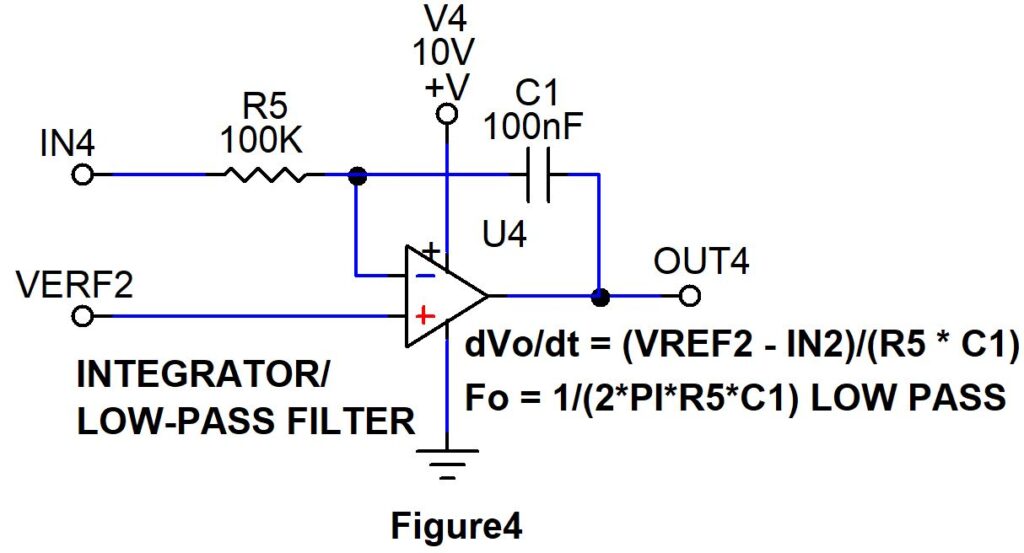
4. Integrator/ Low pass filter
The fourth basic op amp circuit is the integrator/ low-pass filter. When square wave signal is fed into its input, the output will be a sawtooth wave. The following discussion references the circuit in Figure 4. When an input signal is applied at IN4, current flows through R5. VERF2 can be connected to ground or any other reference voltage.
This is a negative feedback setup of Op amp. When the momentary step input at IN4 is high and VERF2 is tied to ground, the Capacitor C1 will be in uncharged state and therefore maximum current flows through it and Capacitor starts charging. Now we know in negative feedback setup Operational amplifier will take measures to equalize voltages at both negative and positive input. Therefore zero current flows to negative input of Op amp and voltage at this point will be zero.
The output of Op amp at this point will be low or zero. Once voltage across capacitor starts building up the charging current reduces and the voltage across capacitor will be equal to the step input voltage. Now voltage starts developing at negative input of Op amp and in an attempt to equalize it to its positive input, output will start going high in a linear fashion and charging capacitor.
When capacitor reaches voltage that is equivalent to OUT4, voltage at Op amp output will start ramping down. The cycle repeats to generate sawtooth waveform it the output.
Charging and discharging of capacitor C1 in a linear fashion results in saw tooth generation. This is given by the formula
dVo/dt = (VREF2 – IN2)/(R5 * C1).
The ramp rate is dVo/dt is the change in output voltage versus the change in time. When either R5 or C1 is decreased, this will increase the ramp rate of the output at OUT4.
If a sinusoidal signal is input into IN4, the circuit acts as a low-pass filter. Frequencies below the corner frequency, Fo will pass with little to no attenuation. Frequencies above the corner frequency, Fo are attenuated by 6 decibels per octave. The corner frequency is given by the equation,
Fo = 1/(2*PI*R5*C1).
When either R5 or C1 is decreased, the corner frequency is increased.
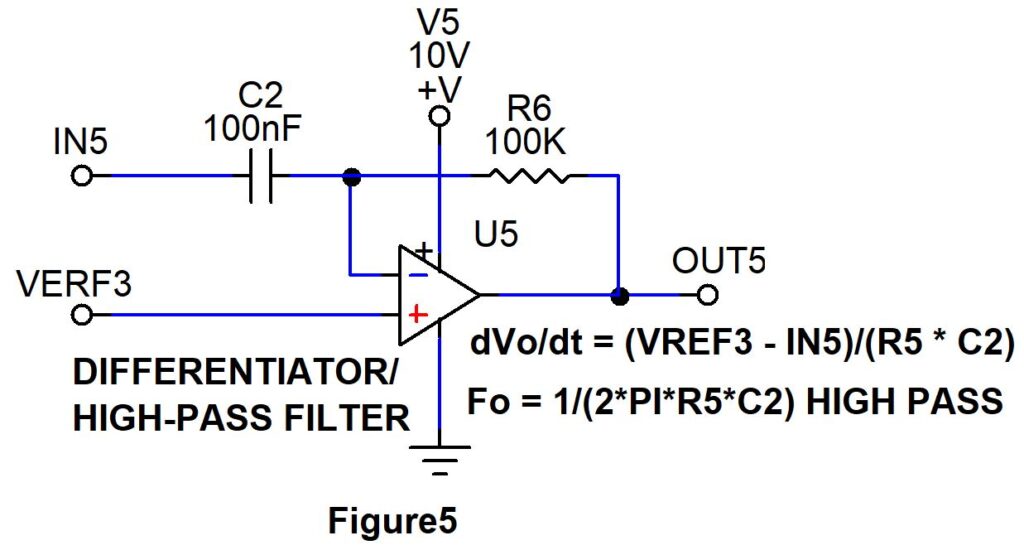
5. Differentiator / High pass filter
The fifth basic op-amp circuit is the differentiator/high-pass filter. Figure 5 shows the circuit for the following discussion. Let’s say VERF3 is connected to ground and square wave is used as signal input to IN5.
When high logic or level 1 signal is applied at IN5 high current flows through C2 and charge the capacitor. Now a voltage potential will be developed across R6. Since it is a negative feedback configuration Op amp output will try to bring equalize the voltage at both inverting and non-inverting terminals. Therefore negative voltage spike will occur at OUT5 output allowing the current flow through it until capacitor is fully charged.
When the signal switches to low logic, capacitor C2 will be discharged through IN5. Now OUT5 will exhibit a positive voltage spike to force the current through IN5 and equalize the voltages at inverting and non inverting terminal.
Thus, a step voltage input (square signal ), produces voltage spike output at OUT5. If a sinusoidal signal is input into IN5, the circuit acts as a high-pass filter. Frequencies above the corner frequency, Fo, pass with little to no attenuation.
Frequencies below the corner frequency, Fo, are attenuated by 6 decibels per octave. The corner frequency is given by the equation,
Fo = 1/(2*PI*R6*C2).
When either R6 or C2 is decreased, the corner frequency is increased.
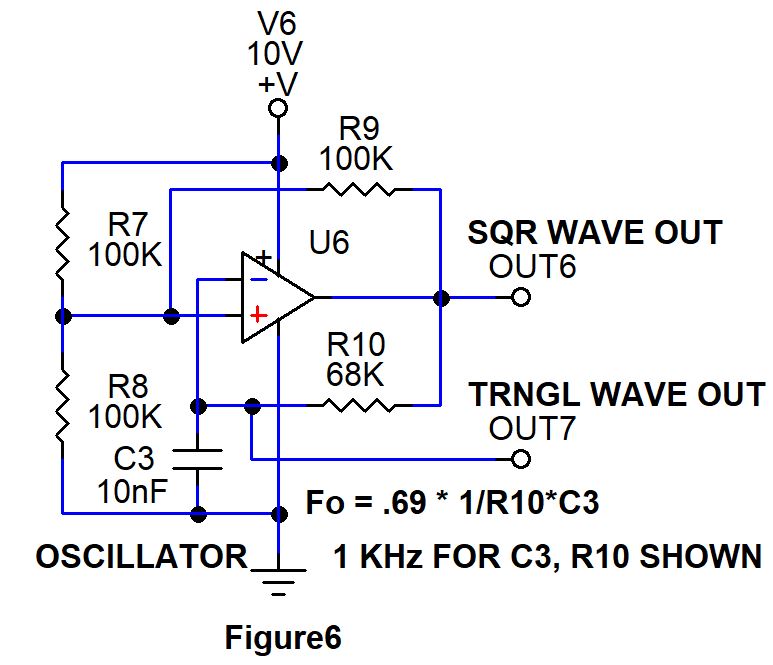
6. Oscillator
The sixth basic op-amp circuit is the oscillator. Refer to Figure 6 for the following discussion. The oscillator in Figure 6 provides two outputs, a square wave output at OUT6 and a triangle wave output at OUT7.
Initially the input to non inverting terminal is at Vs/2 which is 5v. Let’s assume the capacitor is at uncharged state therefore voltage to inverting input is zero. This forces the output of Op-amp to high state or at Vs. When the output of the Op-amp is equal to Vs, then feedback resistor R9 will be parallel with R7 since both voltage applied across both the resistors will be equal to Vs.
Vo = Vs. ( R8 / ( R8 + R7 || R9)
= Vs. ( 100k / 100k + 50k )
= 2Vs/3
This forces the positive input of Op-amp to 2Vs/3, High state of Op-amp output forces C3 to charge up through R10 till voltage at inverting input of Op-amp input exceeds 2Vs/3. Now op-amp switches its output to ground, now Resistor R8 and R9 will be in parallel since both are connected to ground. Applying that in voltage divider formula
Vo = Vs. ( R8 || R9 / ( R8 || R9 + R7 )
= Vs. ( 50k / 100k + 50k )
= Vs/3
causing the positive op-amp input to switch to Vs/3. Resistor R10, discharges C3 until the negative op amp input goes below Vs/3. Thus the voltage at the positive input of the op-amp is switched between 2Vs/3 and Vs/3. The amount of hysteresis is the difference of these two values, or Vhys = 2Vs/3 – Vs/3 = Vs/3.
The Op amp output switches between Vs and 0 with a short time duration between them thus creating a square wave pulse in the output. Meanwhile R10 and C3 ramp up and down resulting in creating a triangle wave across capacitor C3.
The frequency of the output signal can be determined by the formula Fo = 0.69 x 1 / R10 x C3. This gives a output frequency signal of 1kHz for this circuit.
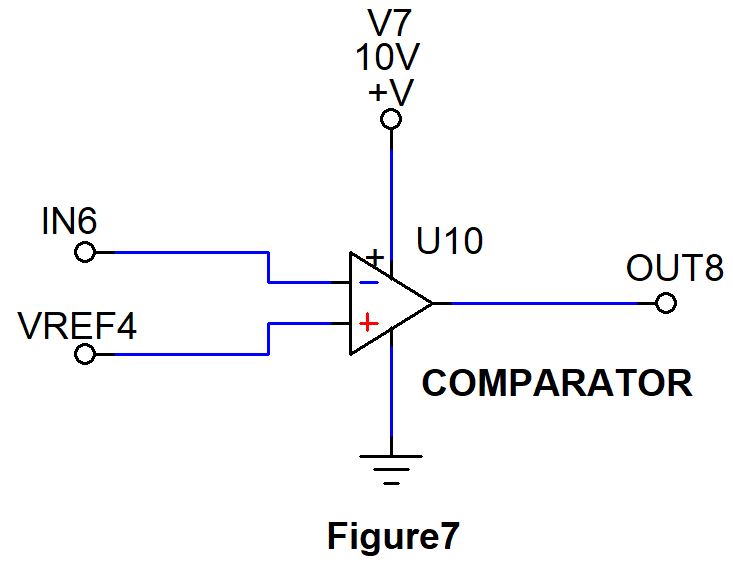
7. Comparator
The seventh basic op-amp circuit is the comparator. Use Figure 7 for the following discussion. With no feedback provided from the output OUT8 to the negative input IN6, the op-amp functions as a comparator. This means the voltage applied across non inverting and inverting terminal will be compared and output will change accordingly.
When IN6 is less than VREF4, the op-amp will be equal V7 which is +10v, minus the output stage limit. This is because Op amp outputs will not achieve full swing to the supply voltage when exhibiting high logic, rail to rail Op amps exhibit output that is close to supply voltage but still short in matter of millivolts from supply voltage.
When IN6 is greater than VREF4, the op-amp output will be equal to ground, (plus the output stage limit). In this case the output of Op amp will be not be really zero but close to zero.
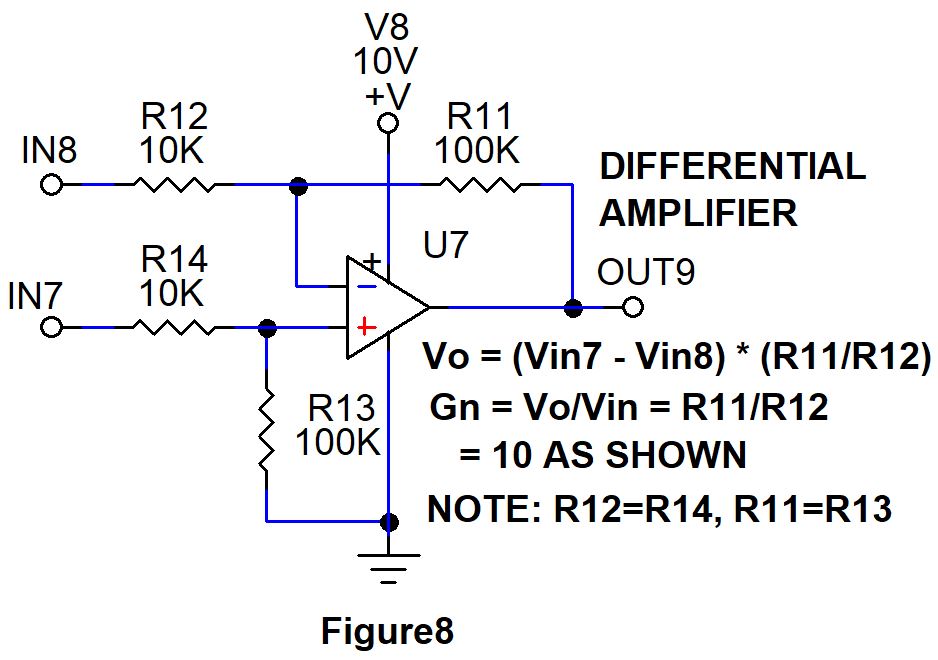
8. Differential amplifier
The eighth basic op-amp circuit is the differential amplifier. Differential amplifiers are often used for amplifying bridged sensors, like in pressure sensors, strain gauge weight measurement sensors. They are used for amplifying bio-electric signals, such as EEG (Electro-EncephaloGraph) and EKG/ECG (Electro- CardioGraph).
Differential amplifiers are used for thermocouples, and other isolated differential signal sources, like a low-impedance balanced line dynamic microphone. Basically differential amplifier amplifies the difference in signal amplitude that is applied between two terminals.
Refer to Figure 8 for the following discussion.
To explain the operation of the differential amplifier shown in Figure 8, let us supply a .1 volt source between IN7 and IN8 with the positive connected to IN7.
If IN8 is referenced to ground, then the voltage at positive terminal of Opamp can be determined using voltage divider formula
Op amp positive terminal is = ( 100K/100K + 10K )* .1V = .09091 volts.
Since the IN8 is at ground, Op amp negative terminal must be equal to .09091volts as well. Remember the negative feedback will force voltage at negative and positive terminal of Op amp to be equal.
Now the current through R12 and R11 must equal since both are in series
I = .09091/10K = 9.091 uA.
We can deduce voltage across R11 by using Ohms law
V= 9.091 uA * 100K = .9091 volts.
Summing these voltages – the voltage at Op amp – which is .09091 volts, and voltage across R11 which is 0.9091 volts will give the output voltage at OUT9
.9091V + .09091V = 1 volt which gives a gain of 10.
Thus you can see this circuit amplifies the difference between input voltage applied across IN7 and IN8 which is 0.1V to 1V at output.
Hope this article gives you the basics to design operational amplifier circuits you can use in your projects. There are many other useful circuits that are more complicated and use two or more op-amps.