Merge sort Algorithm explained

Sorting algorithms are the ones used by programmers to sort elements in an array based on the need for programmer. There are many sorting algorithms that can help programmer to perform this task such as Bubble sort, Insertion sort, Selection sort etc. Adding to this list is the Merge sort algorithm which sorts the elements in an array by splitting the array in to chunks and then merging them in the sorted form.

Merge sort Algorithm explained:

When sorting an array using Merge sort algorithm the array will be divided into equal partitions. Then the elements in the array are merged by sorting the elements and positioning them in right order to get a fully sorted array. To explain this better take a look at the below example

Let us consider the following array and sort the elements in the ascending order using merge sort.

Now the array with eight elements divided into two partitions with four elements in each partition.

Now both the partitions are again divided into equal partitions as the numbers in both the partitions are not sorted.

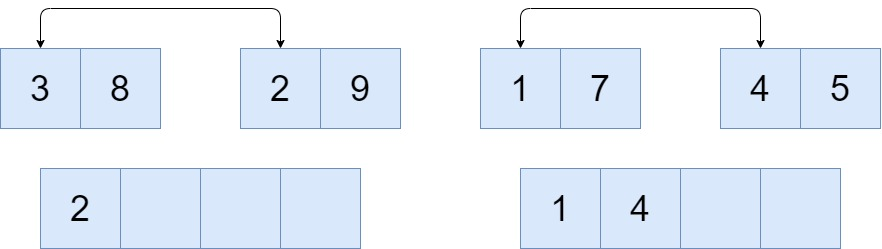
Again the four partitions are divided into eight as a single block with one number

Now, every number is merged by comparing it with the other and based on the order they are copied accordingly into the new block.

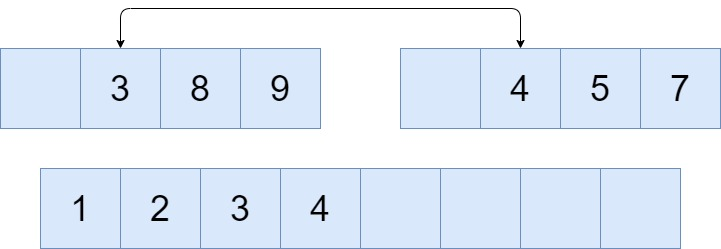
To merge these blocks every element in the first block is compared with all the other elements in the second block and are placed accordingly in the sorted order in the new merged block.

Now the comparison of elements with other set are done and elements are placed accordingly, in the new merged block

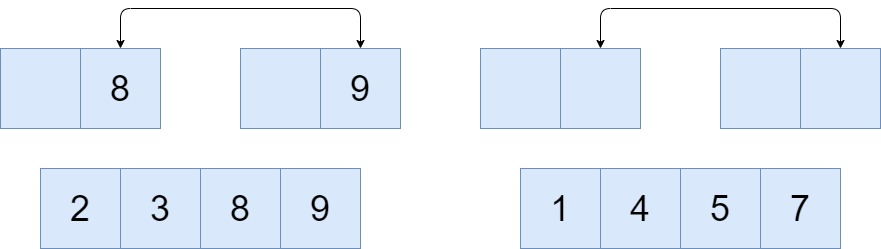
Finally after comparison each and every element with other two merged blocks are obtained

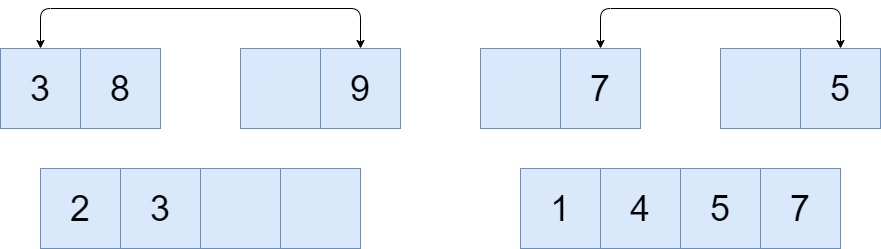
The blocks are merged by comparing each and every element of the block with all the elements of another block and are placed accordingly in the final block.

The comparison of the elements is done recursively in the similar way and finally the list of numbers in the array is obtained in the sorting order.

Steps to implement Merge sort Algorithm:

1. Let us consider array A[0…..n-1]. Split this array A into two equal partitions and consider the two partitions as array B and C.
2. Split the arrays B and C recursively until an array with one element is obtained.
3. Now merge the two arrays of single elements, by comparing all the numbers in one block with all the elements in the another block and the elements are placed accordingly in the merged block based on ascending order sorting obtained by comparison.
4. Now this method of sorting elements by comparing and merging has to be done recursively.
5. Finally the array A[0…..n-1] with the numbers in the ascending order will be obtained

Sample code:

#include<stdio.h>
 
void mergesort(int a[],int i,int j);
void merge(int a[],int i1,int j1,int i2,int j2);
 
int main()
{
   int a[30],n,i;
   printf("Enter no of elements to sort:");   
   scanf("%d",&n);
   printf("Enter the elements:");
   
   for(i=0;i<n;i++)
      scanf("%d",&a[i]);
      
   mergesort(a,0,n-1);
   
   printf("\nSorted array is :");
   for(i=0;i<n;i++)
      printf("%d ",a[i]);
      
   return 0;
}
 
void mergesort(int a[],int i,int j)
{
   int mid;
      
   if(i<j)
   {
      mid=(i+j)/2;            //middle elements        
      mergesort(a,i,mid);     //left recursion
      mergesort(a,mid+1,j);	//right recursion
      merge(a,i,mid,mid+1,j);	//merging of two sorted sub-arrays
   }
}
 
void merge(int a[],int i1,int j1,int i2,int j2)
{
   int temp[50];	//array used for merging
   int i,j,k;
   i=i1;	//beginning of the first list
   j=i2;	//beginning of the second list
   k=0;
   
   while(i<=j1 && j<=j2)	//while elements in both lists
   {
      if(a[i]<a[j])
         temp[k++]=a[i++];
      else
         temp[k++]=a[j++];
   }
   
   while(i<=j1)	//copy remaining elements of the first list
      temp[k++]=a[i++];
      
   while(j<=j2)	//copy remaining elements of the second list
      temp[k++]=a[j++];
      
   //Transfer elements from temp[] back to a[]
   for(i=i1,j=0;i<=j2;i++,j++)
      a[i]=temp[j];
}

Try this out:

• Use merge sort algorithm to sort 11 elements in an array.